C12. 1 Rotational Motion

 C12.1 Rotational Dynamics

Rigid body

Rigid bodies are those solid bodies in which molecules are tightly packed and small inter-molecular distance with definite shape. The inter-molecular distance between two particles remain unchanged due to external forces i.e even on application of force, their configuration do not change during linear and rotational motion.

Rotational motion is the type of motion in which a body moves about any given axis. During rotational motion, the angular velocity of all the particles of a body are same whereas their linear velocity is different. However no real body is perfectly rigid practically. But for all practical purposes, all solids can be regarded as rigid bodies. A rigid body can undergo both transnational and rotational motion.

A rigid body is said to have translatory motion if it moves bodily from one place to another. Every particle in it suffers the same displacement. Similarly, a rigid body is said to be in rotational motion about a fixed axis when its particles generate concentric circles withe the same angular velocity but different linear velocity. For example , Rotation of fan, rotation of the earth, spinning top, etc.

Equations of angular motion

The rotation motion of a rigid body about an axis is described by an angular displacement \(\theta\). Every particles has its own linear displacement that is represented by s, the relation between angular and linear displacement is  

 \[s = r \theta........(i)\]

a                                                                                           b

Angular velocity of the rigid body when the angular displacement \(d\theta\) in the time interval dt is: 

\[\omega = \frac {d\theta}{dt}..........(ii)\]

As the angular velocity is not uniform, the angular acceleration \(\alpha\) is given by,

\[\alpha = \frac {d\omega}{dt}............(iii)\]

The liner velocity  v of the the particle of the rigid body is tangent along the curved path. The relation between linear and angular velocity is given by,

Using equation (i) and (ii), we get,

\[\omega = \frac {d\theta}{dt}\]

Putting the value of \(\theta \) from equation (i)

 \[or,\omega = \frac {d ({\frac{s}{r}})}{dt}\]

 \[or, \omega = \frac {1}{r} \frac{ds}{dt}\]

 \[or, \omega = \frac {1}{r} v\]

\[\therefore v =r\omega............(iv)\]

Again,

From equation (iii) and (iv)

\[\alpha = \frac {d\omega}{dt}\]

 \[or, \alpha = \frac {d (\frac {v}{r})}{dt}\]

 \[or, \alpha = \frac {1}{r} \frac{dv}{dt}\]

\[or, \alpha = \frac {1}{r} a\] 

\[\therefore a = r\alpha\]

First Equation

Consider a rigid body rotating about a fixed axis with angular acceleration '\(\alpha \)' and 'd\(\omega\)' be the change in angular velocity in time 'dt'. By the definition of angular acceleration of a rigid body,

\[\alpha  = \frac{{d\omega }}{{dt}}\]

\[\alpha .dt = d\omega \]

Integrating both sides, we get

\[\alpha \int {dt}  = \int {d\omega } \]

\[\alpha . t + c = \omega............(i)\]

At time t = 0,  \[\omega  = {\omega _0}\]

Using in equation  (i)

\[\alpha . 0 + c = {\omega_0}\]

\[{\omega _0} = c\]

Using this value in equation (i)

\[\omega ={\omega_0} +{\alpha}t................(ii)\]  

Second equation:

Let \(\omega\) be the angular velocity of a rigid body at any instant of time t, then by the defination of angular velocity,

\[\omega =\frac{{d\theta }}{{dt}}\]

or, \[d\theta = \omega dt..............(iii)\]

At t = 0, \(\theta\) = 0

At t = t, let \(\theta\) = \(\theta\)

Integrating equation (iii) in the limit of time and angular displacement, we get,

\[\int\limits_0^\theta  {d\theta  = \int\limits_0^t {\omega dt} } \]

\[or,\int\limits_0^\theta {d\theta = \int\limits_0^t{\omega_0 + \alpha t dt}}\]

\[or,\int \limits_0^\theta d\theta =\int\limits_0^t dt +\alpha \int\limits_0^t tdt \]

\[\left[ \theta  \right]_0^\theta  = {\omega _0}\left[ t \right]_0^t + \alpha \left[ {\frac{{{t^2}}}{2}} \right]_0^t\]

\[\left[ {\theta  - 0} \right] = {\omega _0}\left[ {t - 0} \right] + \frac{\alpha }{2}\left( {{t^2} - 0} \right)\]

\[\theta  = {\omega _0}t + \frac{1}{2}\alpha {t^2}............(iv)\]

Third equation of motion: 

Angular acceleration \(\alpha\) may be expressed as : 

\[\alpha  = \frac{{d\omega }}{{dt}} = \frac{{d\omega }}{{d\theta }}.\frac{{d\theta }}{{dt}} = \frac{{d\omega }}{{d\theta }}\omega \]

\[\omega d\omega  = \alpha d\theta .................(v)\]

At t=0, \(\theta\) = 0  and \(\omega\)=\(\omega_0\) (initial angular velocity)

At t = t, \(\theta\) = \(\theta\) and \(\omega\)=\(\omega\) (final angular velocity)

Integrating equation (v) within the limits of \(\theta\) and \(\omega\), we get 

\[\int\limits_{{\omega _0}}^\omega  {\omega d\omega }  = \int\limits_0^\theta  {\alpha d\theta  = \alpha \int\limits_0^\theta  {d\theta } } \]

\[\left[ {\frac{{{\omega ^2}}}{2}} \right]_{{\omega _0}}^\omega  = \alpha \left[ \theta  \right]_0^\theta \]

\[\frac{{{\omega ^2}}}{2} - \frac{{\omega _0^2}}{2} = \alpha (\theta  - 0)\]

\[{\omega ^2} - \omega _0^2 = 2\alpha \theta \]

Moment of inertia: 

From the Newton's law of motion, inertia is the property of an object by virtue of which the object is unable to change its state of rest of uniform linear motion. So, the greater the mass of the object, the greater the force required to produce the linear acceleration in the object i.e inertia is directly proportional to the mass of the object. 

Similarly, in case of rotational motion of an object about an axis is unable to change its rotational motion. This inability of the rotating body is called rotational inertia or moment of inertia. Therefore moment of inertia is analogous to the mass in linear or transnational motion. 

Moment of inertia is the rotational inertia of a rotating body about a fixed axis that opposes any change in the state. Moment of inertia is not constant, but its value varies with the axis of rotation chosen and the distribution of mass of the body.  Mathematically it the product of mass of a body (m) and square of the distance of the mass from the axis of rotation (r). So,

Moment of inertia of a rotating body about a fixed axis (I) =mr² . Its SI unit is Kgm² . Its dimensional formula is [ML²T⁰]. 

Consider a body having 'n' particles of masses m₁,m₂, m₃, ...............m_n, which are at distance r₁, r₂, r₃.................r_n from the axies of rotation YY' as shown in the figure. Now, moment of inertia of particle of mass m₁ is,

I₁=m₁r₁²

I₂ = m₂r₂²

Similarly, 

I_n = m_nr_n²

Now, Total moment of inertis is,

I = I₁ + I₂ + I₃.............I_n

I = m₁r₁² + m₂r₂² + ................ + m_nr_n²

\[I = \sum\limits_{i = 1}^n {{m_i}} r_i^2\]

[Moment of inertia plays the same role in rotational dynamics like mass does in transnational motion.]

Kinetic Energy of rotating body: 

Let us suppose a rigid body of mass M is rotating about an axis YY'. The angular velocity of the body about the axis is \(\omega\). If \({m_1} {y_1}^2\). If \(m_1\) , \(m_2\) , \(m_3\) ............\(m_n\) are the masses of particles of the rigid body at distance \(r_1\) , \(r_2\) ,\(r_3\) ................\(r_n\) respectively from the axis YY'. Here, each particles has same angular velocity but different linear velocity, since each particles are different distance from the rotational axis. 

Let the linear velocities of masses \(m_1\) , \(m_2\) , \(m_3\) ............\(m_n\) be  \(v_1\) , \(v_2\) ,\(v_3\) ................\(v_n\) respectively. Then, 

\(v_1 =\omega r_1\), \(v_2 =\omega r_2\), \(v_3 =\omega r_3\),.................., \(v_n =\omega r_n\)

When a body rotates about the axis, it possesses rotational K.E. 

Rotational kinetic energy of mass \(m_1\) = \(\frac {1}{2} m_1 (v_1)^2 \) = \(\frac {1}{2} m_1 (\omega r_1)^2 \) = \(\frac {1}{2} m_1 {\omega}^2 {r_1}^2 \) 

Rotational kinetic energy of mass \(m_2\) = \(\frac {1}{2} m_2 (v_2)^2 \) = \(\frac {1}{2} m_2 (\omega r_2)^2 \) = \(\frac {1}{2} m_2 {\omega}^2 {r_2}^2 \) 

:

:

:

Rotational kinetic energy of mass \(m_n\) = \(\frac {1}{2} m_n (v_n)^2 \) = \(\frac {1}{2} m_n (\omega r_n)^2 \) = \(\frac {1}{2} m_n {\omega}^2 {r_n}^2 \) 

Total rotational kinetic energy of the rigid body is equal to the sum of the kinetic energy of all the particles of the rotating body,

Rotational KE of the body =  \(\frac {1}{2} m_1 {\omega}^2 {r_1}^2 \) + \(\frac {1}{2} m_2 {\omega}^2 {r_2}^2 \)  +  \(\frac {1}{2} m_3 {\omega}^2 {r_3}^2 \) +........

or, KE = \(\frac {1}{2} (m_1 {r_1}^2 + m_2 {r_2}^2 + m_3 {r_3}^2 + ............){\omega}^2\) 

or, KE= \(\frac {1}{2} \sum\limits_{i=1}^n  {(m_i {r_i}^2)} {\omega}^2\)

\(\therefore \) KE= \(\frac {1}{2} I {\omega}^2\) 

Where, \(I = \sum\limits_{i = 1}^n {{m_i}} r_i^2\) moment of inertia of the rigid body about YY' axis. 

Above equation is analogous to the transnational kinetic energy  (\(\frac {1}{2}{m}{v}^2\) ) of the body. 

Radius of Gyration (K):

Radius of gyration is defined as the perpendicular distance between the axis of rotation and the point where all the mass of the body is supposed to be concentrated (centre of mass).

Consider a body of 'n' particles having masses m₁ m₂........... m_n at distances r₁, r₂, .......r_n  from axis of rotation. Let M be the total mass of the body and K be the Radius of gyration. 

Now Moment of Inertia 

\[I = M{K^2}.........(i)\]

Also, 

\[I = {m_1}r_1^2 + {m_2}r_2^2 + ......... + {m_n}r_n^2........(ii)\]

From equation (i) and (ii)

\[M{K^2} = {m_1}r_1^2 + {m_2}r_2^2 + ......... + {m_n}r_n^2\]

Let, 

\[m = {m_1} = {m_2} + ......... + {m_n}\]

Also,

                                    M = nm

Now, 

\[mn{K^2} = m({r_1^2} + {r_2^2} + {r_3^2} + ......... + {r_n^2})\]

\[{K^2} = \frac{{(r_1^2 + r_2^2 + r_3^2 + ......... + r_n^2)}}{n}\]

\[{K^2} = \sqrt {\frac{{(r_1^2 + r_2^2 + r_3^2 + ......... + r_n^2)}}{n}} \]

1. Moment of inertia of thin uniform rod: 

a. About an axis through its centre of mass and perpendicular to it:

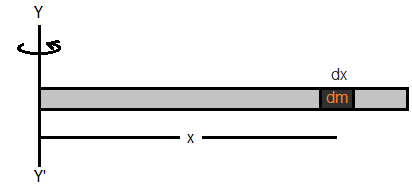
Consider a rod & mass 'm' and length 'l'. Let dx be a small length at a distance 'x' from the axis of rotation passing through the centre of mass as show in the figure above.

Now,

Mars per unit = M /l

The mass of length dx is (dm)= dx (M/l) then, the moment of inertia of this mass is given by;

dI = dmx²

Total moment of inertia of the rod is, 

\[I = 2\int\limits_0^{{\textstyle{l \over 2}}} {dm.{x^2}} \]

\[ = 2\int\limits_0^{{\textstyle{l \over 2}}} {{x^2}\frac{M}{l}dx} \]

\[ = 2\frac{M}{l}\int\limits_0^{{\textstyle{l \over 2}}} {{x^2}dx} \]

\[ = 2\frac{M}{l}\left[ {\frac{{{x^3}}}{3}} \right]_0^{{\textstyle{l \over 2}}}\]

\[ = \frac{2}{3}\frac{M}{l}\left[ {{{\left( {{\textstyle{l \over 2}}} \right)}^3} - {{\left( 0 \right)}^3}} \right]\]

\[ = \frac{2}{3}\frac{M}{l}\frac{{{l^3}}}{8}\]

\[ = \frac{1}{{12}}\frac{M}{l}{l^3}\]

\[\therefore I = \frac{1}{{12}}{M}{l^2}\]

b. About an axis through one end: 

Consider a thin uniform rod of mass 'm' and length 'l'. Let y y' be an axis through one end. Let 'dx' be a small length at a distance 'x' from the axis of rotation as shown in the figure above. Now,

Mass per unit length = \(\frac{M}{l}\)

and Mass of length dx is \[dm =dx.\frac{M}{l}\]

Now, The moment of inertia of mass dm is given by, 

\[dI = dm{x^2}\]

^{Then, Total moment of inertia of the body is given by,}

^{\[I = \int\limits_0^l {dm{x^2}} \]}

\[ = \int\limits_0^l {\frac{M}{l}{x^2}} dx\]

\[ = \frac{M}{l}\int\limits_0^l {{x^2}} dx\]

\[ = \frac{M}{l}\left[ {\frac{{{x^3}}}{3}} \right]_o^l\]

\[ = \frac{M}{{3l}}{l^3}\]

\[ = \frac{1}{3}M{l^2}\]

\[\therefore I = \frac{1}{{3}}{M}{l^2}\]

2. Moment of inertia of a ring:

a. About an axis perpendicular and passing through centre: 

Let us consider a circular ring of radius 'r' and mass 'M'. YY' is the axis perpendicular to its plane passing through the centre of the ring. and dx be the small length at point 'r' from axis of rotation. 

Then mass per unit length of the ring is given by, 

Mass per unit length =\(\frac{M}{2\pi r}\)

Then, mass of the small length is,

\[dm = \frac{M}{2\pi r} dx\]

Moment of inertia of elementary portion is,

\[dI = dm.r^2\]

\[= \frac {M}{2 \pi r} . dx.r^2\]

\[= \frac{Mr}{2\pi}. dx ............(i)\]

The total moment of inertia of circular ring, axis passing through the centre and perpendicular to its plane is calculated by integrating equation (i) from 0 to 2\(\pi\)r. 

\[I = \int\limits_0^{2\pi r} {dI} \]

\[I = \int\limits_0^{2\pi r} \frac{Mr}{2\pi}dx \]

\[I = \frac {M}{2\pi} \int\limits_0^{2\pi r} r dx\]

\[I=\frac {Mr}{2\pi} \int\limits_0^{2\pi r} dx\]

\[I = \frac{{Mr}}{{2\pi }}\left[ x \right]_0^{2\pi r}\]

\[I= \frac{{Mr}}{{2\pi}}\left[2\pi r - 0 \right]\]

\[\therefore I=Mr^2\]

Which is the expression for the moment of inertia of circular ring about an axis perpendicular to the plane passing through centre. 

3. Moment of inertia of a circular disc about an axis passing through centre and perpendicular to the plane of the disc: 

Consider a circular disc having radius 'r' and mass 'M'. Then, mass per unit area of the disc is 

 Mass per unit area \(=\frac{M}{\pi r^2}\). 

Let, YY' be the axis passing through the center of disc perpendicular to its plane. A disc consists a number of concentric circles, among them dx be the width of elementary portion at a distance x from axis of rotation. 

Then, area of elementary portion (da) = dx\(\times 2\pi x\)

And, mass of the elementary portion (dm) = \(\frac {M}{\pi r^2} \)da

Moment of inertia of elementary portion is,

\(dI=dm.x^2 \)

\(dI=\frac{2Mx}{r^2} dx. x^2\)

\(dI = \frac{2Mx^3}{x^2} dx..........(i)\)

Now, 

The total moment of inertia of circular disc about YY' perpendicular to the plane of the disc is obtained by integrating equation (i) from 0 to r. 

Total moment of inertia of the disc \(I= \int\limits_0^r dI\)

\[I=\int\limits_0^r \frac {2Mx^3}{r^2} dx\]

\[I=\frac{2M}{r} \int\limits_0^r x^3 dx \]

\[I =\frac{2M}{r^2} \left[\frac{x^4}{4}\right]_0^r \]

\[I =\frac{2M}{r^2 4}\left[r^4 - r^0\right]\]

\[I =\frac{M}{2r^2}r^4 \]

\[\therefore I =\frac{Mr^2}{2}\]

This is the expression for the moment of inertia of a circular disc about an axis perpendicular to the the plane of the disc passing through the centre. 

Moment of inertia of some solid objects: 

a. Moment of inertia of a solid sphere: \(I=\frac{{2}{5}} mR^2\)

b. Moment of inertia of hollow sphere: \(I=\frac{{2}{3}} mR^2\)

c. Moment of inertia of a solid cylinder: \(I=\frac{{1}{2}} mR^2\)

d. Moment of inertia of hollow cylinder : \(I =mR^2\)

e. Moment of inertia of rectangular plate with perpendicular axis through centere: \(I=\frac{{1}{2}} m{a^2 + b^2}\)

Theorm of parallel axis :

Theorem of parallel axis states that "The moment of inertia of a body about any axis parallel to the axis passing through centre of mass is equal to sum of moment of inertia of axis passing through center mass and product of mass of body and square of perpendicular distance between two axes"

i.e,

\[I = {I_{cm}} + M{r^2}\]

fig

Proof,

Suppose a solid body with two axes, PQ about which the moment of inertia of the body I is to be determined and RS is another axis passing through the centre of mass O which is parallel to the PQ. Let r be the distance between the Axis PQ and RS as shown in the figure above. 'm' is the mass of the particle at a distance 'x' from the axis RS.

Then, the moment of inertia of the particle with mass 'm' about axis PQ is, \(I = m(x + r)^2\)

Moment of inertia of the whole body about PQ is,

\[I = \sum {m(x + r)^2} \]

\[I = \sum {mx^2 + 2\sum {mxr}  + \sum {mr^2} } \]

As \(I_{cm} = \sum {mx^2}\), the moment of inertia of the body about the axis RS i.e axis through centre of mass, then

\[I = I_{cm} + \sum {Mr^2} + 2 \sum {m} xr..........(i)\]

Here, \(\sum {mr^2} = r^2 \sum {m} = Mr^2\) and M is the total mass of the body. \(\sum {mx}= \) the sum of the moments of all the particles of the body about the axis RS passing through the centre of mass which is is equal to zero i.e \(\sum {mx}=0\). Then from equation (i), we have 

\[I= I_{cm} + {Mr^2}...............(ii)\]

Equation is the moment of inertia of the body abut the axis PQ which is the sum of the moment of inertia about a parallel axis RS through centre of mass and the product of mass of the body and square of the distance between the axes. 

Theorem of of perpendicular axis: 

Theorem of perpendicular axis states that "The moment of inertia of any axis in a thin lamina is equal to sum of moment of inertia of two mutually perpendicular axes passing through intersection of two mutually perpendicular axes and perpendicular to its plane"

Let \(I_{x}\), \(I_{y}\) and \(I_{z}\) be the moment of inertia of the plane lamina about three mutually perpendicular axes passing through the point O. XO and YO are in the plane and ZO is perpendicular axis to the plane of lamina. Then,

\[I_{Z} = I_{x} +I_{y}\]

Fig

Suppose, OX and OY be the mutually perpendicular axes in the plane of lamina. \(m_1\) is the mass of a particle at a distance \(r_1\) from the intersection point O. The particle is \(x_1\) and \(y_1\) distance from X-axis and Y-axis respectively. Moment of inertia of the \(m_1\)  about Y-axis is \({m_1} {y_1}^2\). If \(m_1\) , \(m_2\) , \(m_3\) ............\(m_n\)  are the masses of particles at distance \(r_1\) , \(r_2\) ,\(r_3\) ................\(r_n\) respectively from point O. These masses are are at a distance of \(x_1\) , \(x_2\) ,\(x_3\) ................\(x_n\) from Y-axis and \(y_1\) , \(y_2\) ,\(y_3\) ................\(y_n\) from X-axis respectively. Then, 

Moment of inertia of the lamina about X-axis \({I_x} = {m_1}{y_1}^2 + {m_2}{y_2}^2 +{m_3}{y_3}^2 + ...............+{m_n}{y_n}^2\) = \(\sum m{y}^2\)

Similarly, Moment of inertia of the lamina about Y-axis \({I_y} = {m_1}{x_1}^2 + {m_2}{x_2}^2 +{m_3}{x_3}^2 + .............+{m_n}{x_n}^2\) = \(\sum m{x}^2\)

Moment of inertia about mutually perpendicular axis with x-axis and y-axis through O is: 

\(I= {m_1}{r_1}^2 + {m_2}{r_2}^2 +{m_3}{r_3}^2 + ..........+{m_n}{r_n}^2\)

 \(I= {m_1}{x_1+y_1}^2 + {m_2}{x_2 +y_2}^2 +{m_3}{x_3 +y_3}^2 + ...........+{m_n}{x_n +y_n}^2\)

 \(I= {m_1}{x_1}^2 + {m_2}{x_2}^2 +{m_3}{x_3}^2 + ........+ {m_1}{y_1}^2 + {m_2}{y_2}^2 +{m_3}{y_3}^2 + .........\)

 \(I= \sum {m}{x}^2 + \sum {m}{y}^2 \)

 \(\therefore I= I_x + I_y\)

Read More

C11. 1. Physical Quantity

 1. Physical Quantity

    Physics is the branch of science that deals with the natural laws in mathematical terms that determine the structure of the universe with reference to the matter and energy contained in it and their interactions. It is so broad that nature and behavior of atoms and subatomic particles and their constituent is studied under quantum mechanics and particle physics to large scale structure of universe, its origin, evolution with time is studied under cosmology and astrophysics. Physics intersects with many other branches of sciences such as biophysics and quantum chemistry, quantum computing, astronomy etc, due to which boundaries of physics has not been rigidly defined. Mathematics is the tool that is used by physicist to have the better understanding of natural phenomena. 

Matter:- Matter is any thing that has mass and occupies space which is composed of atom. It can exist in different sates like solid, liquid, gas, plasma etc. 

Physical quantity: - Those quantities which can be measured directly or indirectly is called physical quantity. Physical quantity obeys the natural laws which can be expressed interms of mathematical relations.

    A physical quantity has two parts i.e numerical values and unit. Numerical value or magnitude gives the quantitative idea of physical quantity. Unite gives idea about the physical quantity. There are two types of physical quantities. They are : 

i. Fundamental Physical quantity: The physical quantity which doe not depend on other physical quantity or the physical quantity which can not be express interms of other physical quantity and taken as stander is called fundamental physical quantities. 

    There are seven basic fundamental quantities. They are length, mass, time, temperature, electric current, luminous intensity and amount of substance and two supplementary fundamental quantities they are plane angle and solid angle. 

    The units of fundamental quantities are called fundamental units. For examples length(m), mass(Kg), time(s), electric current (A), luminous intensity(Cd), temperature(K), amount of substance (mol), plane angle (rad) and solid angle(sr).

ii. Derived physical quantities: The physical quantity which depend on fundamental physical quantity or can be expressed interms of fundamental physical quantity is called derived physical quantity. 

    The units of derived physical physical quantity is called derived units. For example: Velocity(m/s), density(Kg/m³), Specific heat capacity(J/Kg°C) etc. 

Measurement: Measurement is the process of comparing unknown quantity with known physical quantity. Measurement  is the root of science which guides us to learn the truth about the physical phenomena. Measurement is necessary for us in following ways:

i. It helps in selling and buying goods. 

ii. It helps in doing scientific experiments. 

iii. It helps in preparing goods and foods. 

iv. It helps in making medicines. 

v. It helps in constructing roads, buildings, bridges etc. 

Unit: To express any physical quantity, a unit and numerical value is necessary. So, a physical quantity is represented by a number followed by a unit. 

    Unit is defined as the standard quantity interms of which physical quantity of same kind is expressed or measured. 

                Unit = magnitude symbol

System of units: 

a. CGS System: The system of measurement in which length is measured in centimeter (cm), mass in gram(gm) and time in second(s). It is Franch system of measurement. 

b. FPS System: The system of measurement in which length is measured in foot (ft), mass in pound(lb) and time in second(s).It is the British system of measurement. 

c. MKS System: It is matric system of measurement. In this system length is measured in meter(m) in kilogram(Kg) and time in second (s). 

d. SI System: To establish uniformity in measurement all over the world, scientist held the Eleventh General conference on Weights and Measures in 1960 , France and approved seven basic quantities along with their units which is called SI unit. Later two supplementary quantities of angles were added to the system. 

List of SI units: 

Read More

Heat and temperature

4. Heat and temperature

Heat is a form of energy that produces the sensation of warmth and flows from hot body to cold body.  It is produced due to the vibration of molecules. When molecules vibrate faster more heat is produced.
Matter is made up of molecules, these molecules contains energy. When substances are heated, molecules vibrate that increases the kinetic energy of the molecules. In other words when heat is supplied to an object, it increases the amplitude and frequency of vibration of molecules. These vibrating molecules contain kinetic energy called heat energy. Molecules are vibrating rapidly if the body is at high temperature.
The SI unit of heat energy is Joule (J). In CGS system, it is measured in calorie. One calorie is the quantity of heat required to raise the temperature of 1g of water through 1°C.
Heat also can be defined as the sum of the kinetic energy that the molecules of an object possess is called the heat energy of the object. Quantity of heat energy present in an object depends upon mass and average kinetic energy of the molecules. Quantity of heat is directly proportional to the:
i. Average kinetic of molecules of the body.
ii. Mass of a body i.e the total number of molecules that a body contains.
Heat energy has great many applications. It is used for cooking food, propelling and running vehicles, proper amount of heat from sun provides suitable place for living being on earth etc.

Effects of heat:
i. Increase in volume: When an object is heated, its size and volume increases.
ii. Chant in state: On heating, a solid converts into liquid, while liquid converts into vapour.
iii. Rise in temperature: When a body is heated its temperature increases.
iv. Physical change: When a body is heated, physical properties like colour changes.

Temperature: 
The temperature of a body is defined as the degree of hotness or coldness of a body or it can be defined as the average kinetic energy of molecules of the substance.
When two bodies at different temperature are placed in contact the heat flows from the body at higher temperature to the body at lower temperature. Temperature determines the direction of flow of heat energy from one body to another when these are in contact with each other. Thermometer is used to measure the temperature of an object. 

Thermometer: 

The instrument that is used to measure the temperature is called thermometer and the branch of science related to measurement of temperature of a body is called thermometery. There are different types of thermometer, they are liquid thermometer, gas thermometer, resistance thermometer, radiation thermometer, vapour thermometer etc.  

Liquid thermometer are based on the principle of change in volume of a liquid with change in temperature. Mercury and alcohol thermometers are based on this principle. 

Differences between heat and temperature: 

S.no	Heat	Temperature
1	Heat is a form of energy which gives us the sensation of warmth.	It is the degree of hotness or coldness of a body.
2	It is measured in calorie or joule.	It is measured in °C, K etc.
3	Heat flows from a body at higher temperature to a body at lower temperature.	The temperature of two bodies gives the direction of flow of heat.
4	It is the total KE of all the molecules of a substance.	It is the average KE of the molecules.
5.	It is measured by Calorimeter.	It is measured by the thermometer.
6.	It is cause of temperature.	It is effect of heat.

Read More

Energy

Energy: 



Energy is defined as the capacity to do work. Energy is a scalar quantity. The SI unit of energy is joule (J) and erg in CGS system. The amount of energy produced by a body is equal to the amount of work it can do when the energy is released. In nature there exists different forms of energy like mechanical energy, heat energy, light energy, geothermal energy, nuclear energy, tidal energy, wind energy, chemical energy, electrical energy etc.
One joule of energy is the amount of energy which can move an object of weight 1N through 1 meter.
The sun radiates about 27 × 10²³ Kw (or 4×10^26 J/s) of energy per second and earth receives 1.4 Kw of energy per square meter from the sun. Sun is the major source of energy for us  because other form of energy are transformed from the solar energy either directly or indirectly. Energy is produced in the form of heat and light in sun by thermonuclear fusion reaction of hydrogen atoms. Solar energy is the renewable source of energy and it can be used for longer duration.

Law of conservation of energy: 
Law of conservation of energy states that "Energy can neither be created nor be destroyed by it can only be transformed from one form to another.

Sources of energy: 

i. Primary sources: The sources of energy from which we can obtain energy in natural form are called primary sources. Example: wind energy, solar energy, hydro energy, etc.

ii. Secondary sources: The sources of energy which are obtained after modification from the natural form is called secondary sources of energy. Examples: mineral oil, tidal energy etc.

Types of energy: 

i. Renewal source of energy: The sources of energy which can never be used fully are called can be renewed by the natural process are called renewal source of energy. They do not exhaust even after the regular use in a long period of time. E.g: Electricity, wind, geothermal energy, solar energy etc.

a. Solar energy: The energy that is obtained from sun is called solar energy. Solar energy is the best source of energy for all living beings on earth.

ii. Non-renewable source of energy: The sources of energy which can exhaust if once used up fully are called non-renewal source of energy. It takes long period of time to form again. Eg. petroleum oil, coal, natural gas etc.

Difference between renewable and non-renewable source of energy: 

Renewable source of energy	Non-renewable source of energy
1. The source of energy which can never be used up fully and renewed by natural process.	1. The source of energy which exhaust once it is used up fully.
2. They do not get exhausted even if used regularly.	2. They may exhausted due the regular use.
3. Wind energy, solar energy, tidal energy are renewable sources.	3. Petrol, coal and natural gas are the non-renewable source of energy.

Forms of energy and their uses: 
i. Mechanical energy: Mechanical energy is defined as the energy possessed by a moving body or the body resting at a certain place. There are two types of mechanical energy. They are:
   a. Kinetic energy: The energy possessed of a body by virtue of its motion is called kinetic energy. It is written as KE in short. Examples: energy of flowing water, energy of blowing air, energy of a rolling stone, energy of moving vehicles, etc. Let us consider a body with mass 'm' initially at rest is moving with an acceleration 'a', the final velocity of the body moving after certain distance 's' be 'v'. According to the equation of motion:

${{v}^{2}}-{{u}^{2}}=2as$
${{v}^{2}}=0+2as$  [since u=0]
$s=\frac{{{v}^{2}}}{2a}$

Again, KE = work done
                 = $F\times s$
                 = $ma\times \frac{{{v}^{2}}}{2a}$  [Since F = ma and $s=\frac{{{v}^{2}}}{2a}$]
Therefore, KE = $\frac{1}{2}m{{v}^{2}}$
From above equation it is found that KE of an object is directly proportional to the mass and the square of the velocity.

   b. Potential energy: The energy of a body by virtue of its position or configuration is called potential energy. Example: stretched rubber, water stored in a dam, compressed spring etc. In other words when work is done on a body, potential energy is gained i.e the potential energy gained is equal to work done on the body.
If  a body of mass 'm' when it is raised above the ground at certain height 'h' against the gravity, it tendency to fall back to the ground.  The potential energy of the body is equal to the work done in taking the object to height 'h'. Then,
Work done = F × h
                  = mg × h  [f = ma]
Potential energy (PE) = work done in moving the object to the height h.
                                   = mgh.

ii. Nuclear energy: The large amount of energy obtained after fusion or fission of nucleus of an atom or atoms is called nuclear energy.
       a. Nuclear fusion reaction: The reaction in which lighter nuclei fuse together to form a heavy nucleus with release of large amount of energy. The reaction that occur in sun is thermonuclear fusion reaction. Thermonuclear fusion reaction is a process in which two or more nuclei of smaller atoms fuse together to form a heavier atom under high pressure and temperature with the release of huge amount of energy. The reaction that occurs in sun is shown below:

${}_{1}{{H}^{1}}+{}_{1}{{H}^{1}}\xrightarrow{\text{High pressure and themprature}}{}_{1}{{H}^{2}}+{}_{1}{{e}^{0}}+\gamma (energy)$

${}_{1}{{H}^{2}}+{}_{1}{{H}^{1}}\xrightarrow{\text{High pressure and themprature}}{}_{2}H{{e}^{3}}+\gamma (energy)$

${}_{1}{{H}^{2}}+{}_{1}{{H}^{2}}\xrightarrow{\text{High pressure and themprature}}{}_{2}H{{e}^{4}}+\gamma (energy)$

${}_{1}{{H}^{2}}+{}_{1}{{H}^{3}}\xrightarrow{\text{High pressure and themprature}}{}_{2}H{{e}^{4}}+{}_{0}{{n}^{1}}+\gamma (energy)$
${}_{2}H{{e}^{3}}+{}_{2}H{{e}^{3}}\xrightarrow{\text{High pressure and themprature}}{}_{2}H{{e}^{4}}+{}_{1}{{H}^{1}}+{}_{1}{{H}^{1}}+\gamma (energy)$
In short,
$_{1}{{H}^{2}}{{+}_{1}}{{H}^{3}}{{\xrightarrow{\text{High pressure and themprature}}}_{2}}H{{e}^{4}}{{+}_{0}}{{n}^{1}}+\gamma (energy)$
Where,
\[_{1}{{H}^{1}}=\text{Protium,}{{\text{ }}_{1}}{{H}^{2}}=\text{Deuterium, }{}_{1}{{H}^{3}}=\text{Tritium,}{{\text{ }}_{1}}{{e}^{0}}=\text{Positorn,}{{\text{ }}_{0}}{{n}^{1}}\text{= neutron }\]
      b. Nuclear fission reaction: Nuclear fission reaction is the type of reaction in which heavier nucleon disintegrates into lighter fragments with the release of large amount of reaction. With the help of this reaction atomic bomb are made. The nuclear fission reaction of uranium atom is shown below:
$_{92}{{U}^{235}}{{+}_{0}}{{n}^{1}}{{\xrightarrow{{}}}_{56}}B{{a}^{141}}+{}_{36}K{{r}^{92}}+{{3}_{0}}{{n}^{1}}+\gamma (energy)$

iii. Geothermal energy:The heat energy present inside the earth's interior is called geothermal energy. The temperature inside the earth is about 5000°C to 6000°C. When the underground water comes in contact with this huge temperature it changes into steam or hot water. The steam and the hot water is pumped to the earth surface and used to rotate turbine to produce electricity. It is also used to keep house warm.

iv. Hydro-power: The energy that is obtained from the potential and kinetic energy of water is called hydro-power. Hydroelectric energy is the energy generated with the help of water. The water collected in dam or reservoir is made to fall from a certain height through a tunnel or pipe so that the force of falling water turns the turbine which drives the electric generator. With the help of coil and magnetic field electricity is produced. It is the best eco-friendly source of energy. There is wide used of electrical energy because it can be transformed into different other form of energy and apply for different purposes.
Nepal has high potentiality of hydro-power because most of the rivers in Nepal flow from high altitudes with high speed. Nepal has the potentiality of generating About 83000 MW of hydroelectric power. Only few thousands Mega watts of electricity has been produced until now. This clean energy source is boon to our country which boost up the economy if we able to harvest all of the hydroelectric energy.

v. Fossil fuel: Fossil fuel are the energy rich organic materials like oil, coal, natural gas, petroleum etc. which are formed from the dead remaining of plants and animals buried under earth's crust millions years ago. After decomposition the dead remaining turns into fossil fuel which are being used by human nowadays. 

vi. Coal : Coal is defined as an organic sedimentary rock that forms from the accumulation and preservation of dead remaining of plants and animals under the earth crust in a marsh environment. It contains more than 50% of  carbon along with other constituents like hydrogen, oxygen, sulpher etc. 

There are four types of coal on the basis of amount of carbon present in it. They are peat( containing about 50 to 60 percent of carbon), Lignite or Brown coal ( containing 60 - 70 percent of carbon), Sub-Bituminous (containing 70 - 77 percent of carbon), Bituminous ( containing 77 - 89 percent of carbon) and Anthracite or hard coal ( containing 90 - 95 percent of carbon). 
Alternative source of energy:
The cheap and durable source of energy that can be used instead of non-renewable source of energy is called alternative source of energy. Eg: Solar energy, wind energy, tidal energy, biomass etc.

Sun as the ultimate source of energy:

Sun is the main source  of heat and light energy on earth. It radiates about 27×1023 KW energy each second. The average solar energy received by earth every second per 1 sq. meter  is called solar constant and it is estimated to be nearly 1. 4 KWm^-2.  Different types of energy sources in our daily life are the changed forms of solar energy directly or indirectly. Green plants uses sun light to produce food by photosynthesis process. The food produced by plants is consumed by different types of animals to produce energy for their growth and development. Wind blows in the earth's atmosphere due to change in temperature caused by solar energy that helps to run the wind mills and wind turbines. Water cycle maintained by solar energy recharges the under ground water and irrigates the land, runs the electric turbines in hydropower stations. Most of the energy sources that we use today like fossil fuels, bio-fuel, hydroelectricity, tidal energy etc. are dependent upon solar energy directly or indirectly, so, sun is the main source of energy.  

Energy crisis: 
The rate of consumption of the fuel energy is so rapid that they can not last for longer time due to population growth. If the rate of consumption of fuel energy is continuously increases and no other alternative souses of energy are searched, the fuel like petrol, coal diesel, coal, will be finished. This results the world to be in serous problem of energy scarcity. This shortage of energy sources is called energy crisis.

The main causes of energy crisis are:
i. Huge demand of energy sources because of over population.
ii. lack of proper management of non-renewable source of energy.
iii. Over use of non-renewable source of energy.

Ways to solve energy crisis:
i. By using alternative source of energy.
ii. By controlling population growth.
iii. By conserving the existing source of energy.
iv. By proper management of non-renewable source of energy.

Conservation of energy: 
The saving of energy by proper management and utilization to stop the energy crisis is called conservation of energy. Energy can be conserved in the following ways:
i. by using alternative sources of energy.
ii. by promoting the devices which utilize the solar energy, hydro-power, wind energy, tidal energy etc.
iii. by avoiding non-renewable sources of energy as much as possible.

Read More

Pressure

Pressure
Pressure is defined as the force per unit area. It is a scalar quantity. Its SI unit is N/m² or Pascal (Pa). If the force of different magnitude is applied on the same area, the pressure varies. Pressure is  more when more force acts on the body. Likewise, if same force acts on two different areas, the pressure varies. Pressure goes on increasing when force is increased and vice-versa. When force is applied to the small area the pressure and increases when force is applied to a large area.
Let us consider a force 'F' is applied to a certain surface area 'A' , then pressure is directly proportional to the force and inversely proportional to the area of the surface in which the force acts normally. Mathematically,

$P\alpha F$..................(a)

$P\alpha \frac{1}{A}$....................(b)

Combining equation (a) and (b), we get, 

$P\alpha \frac{F}{A}$...............(c)

$P=k\frac{F}{A}$.................(d)

[Where, k is proportionality constant and its value is 1 because when 1 N force is applied in 1 m², the pressure is 1N/m²]

Therefore, 

$P=\frac{F}{A}$....................(e)

Pressure in liquid: 

Let us consider a container with base area 'A' filled with liquid of density 'd'. Let the depth of liquid inside the container be 'h'. 'F' be the force exerted by the liquid on the base of the container which is equal to the weight of the liquid inside the column.

By the definition of pressure,

$P=\frac{F}{A}$..............(a)

$P=\frac{mg}{A}$..............(b) [As, F=mg]

$P=\frac{dvg}{A}$...............(c) [As, d=m/v and m = dv]

$P=\frac{d(A\times h)g}{A}$.........(d) [As, V=A×l]

$P=dgh$.........(e)      

Equation (e) shows that pressure exerted by liquid in a column depends on: 

- density of liquid 'd'

- height of liquid column 'h'

- acceleration due to gravity 'g'

Equation (e) shows that pressure exerted by the liquid is directly proportional to the height of the liquid column, density of the liquid and acceleration due to gravity.

Laws of liquid pressure: 

• Liquid pressure is directly proportional to its density
• liquid pressure at a point is same in all directions within the liquid. 
• Liquid pressure is independent of the shape of the vessel. 
• Liquid pressure is directly proportional to the depth.

Pascal's law:

Pascal's law states that 'Pressure is equally exerted perpendicularly on all directions as pressure is applied at a point on liquid contained in a enclosed container.'
Pascal's law is based on the principle that liquids are in-compressible and liquid transmits pressure equally in all directions. With the help of Pascal's law we can produce large force by applying small forces. In other words Pascal's law amplifies the applied force and helps in doing work. Hydraulic machines were developed on the basis of Pascal's law. Examples of hydraulic machines are hydraulic machine, hydraulic jack and hydraulic lift etc.

Let us consider a F1, F2, F3, and F4 be the forces applied at pistons p1, p2, p3 and p4, at the same time P1,P2, P3 and P4 are the pressures in the respective pistons. According to Pascal's law, pressure at piston p1 is equally distributed in all other pistons. Mathematically,

p1 = p2 = p3 = p4

Similarly, 

$\frac{{{F}_{1}}}{{{A}_{1}}}=\frac{{{F}_{2}}}{{{A}_{2}}}=\frac{{{F}_{3}}}{{{A}_{3}}}=\frac{{{F}_{4}}}{{{A}_{4}}}$

Hydraulic press:

Hydraulic press is a machine that works under the principle of Pascal’s law. It is usually ‘U’ shaped tube filled with liquid and fitted with air tight pistons. It magnifies the applied force. In other words it converts small applied force into large force. When a small force is applied in a piston of small cross-section area, pressure is equally transmitted in all directions; a large force appears over the piston with larger cross-section area.

Hydraulic press

Hydraulic press as a force multiplier:

Let us consider a hydraulic press filled with water and fitted with air pistons P1 and P2 with cross-section area A1 and A2 respectively. Here, area A1 is smaller than area A2.

When force F1 is applied on a small piston in downward direction , it produces force F2 on piston P2 which moves upward direction due to equal transmission of pressure in all direction according to Pascal’s law.

According to Pascal’s law,

Pressure on small cylinder with piston P1 = Pressure on big cylinder with piston P2.

So, P₁ = P₂

Where P₁  and P₂ are pressure on small and big piston.

Or, $\frac{{{F}_{1}}}{{{A}_{1}}}=\frac{{{F}_{2}}}{{{A}_{2}}}$

Or, ${{F}_{2}}=\frac{{{F}_{1}}\times {{A}_{2}}}{{{A}_{1}}}$

Since, A₂ >A₁ then F­₂ >F₁.

Therefore, hydraulic press or hydraulic lift acts as force multiplier. 

Hydraulic brake

A hydraulic brake is a mechanical component used mostly in vehicles which works on Pascals’s law. In consists of a master cylinder filled with a fluid which is attached to the wheel cylinder with the help of a pipe. The wheel cylinder also consists of the same fluid inside it that is connected to the brake shoe. When foot pedal is pressed the piston in master cylinder is pushed inward along with the special fluid. Then the pressure in the master cylinder is transmitted to the wheel cylinder. The pistons in the wheel cylinder apply force to the brake shoe that widens the brake shoe. Widening of break shoe come in contact with the wheel and produces friction. As a result vehicle stops.

Hydraulic brake

Upthrust: 
Thrust is the force acting perpendicular to the surface. Its unit is Newton. Only liquid and gas exerts up-thrust.
We feel easier to lift a bucketful of water until it is under the surface of the water but becomes heavy when it is out of the surface of water. Similarly, we have experienced during swimming it is easier to lift  a friend inside the water but becomes heavy out of the water.  These examples show that when a body is wholly or partially immersed in water, water pushes the body up with certain force. This force is called upthrust.
Upthrust is defined as the upward force exerted by liquid on an object immersed in in the liquid. It is also called buoyant force or bouncy.

How to measure the upthrust:

Let a stone be tied on a string and suspend it with a spring balance, the weight of the stone in the air be w1 N. The weight of the stone will be w2 N when completely immersed inside the water contained in beaker. There is difference between w1 and w2 due the up-thrust exerted by water in upward direction. This difference in weight gives the up-thrust. Mathematically,
Weight of stone air =w1
Weight of stone inside the water = w2
Then,
Up-thrust = Difference in weight in air and water
                = (w1 - w2)N

Archimedes' Principle: 
Archimedes' principle states that when a body is wholly or partially immersed in a liquid, it experiences a loss in wight due to up-thrust which is equal to the weight of the liquid displaced by it.
This principle can be applied for both liquid and gas.

Properties of Archimedes' Principle: 

• This law can be applied for both liquid and gas.
• Archimedes' principle holds true when an object is wholly or partially immersed in liquid. 
• Up-thrust is independent of weight of an object.

Verification of Archimedes' principle: 
Let us tie a stone by a thread with a spring balance. Measure the weight of the stone in the air, let the weight be w1. Insert the stone completely inside the overflow can (Eureka can) filled with water upto the spout. Due to the up-thrust there is loss in weight of the stone, the weight of the stone be w2. At same time place a empty beaker in pan balance just below the spout of overflow can. Consider the weight of the of the beaker be w3. When the stone is inserted into the water it displaces some water which flows out from the spout into the beaker. Let the weight of the displaced water and beaker be w4. Then,

Loss in weight of the stone in water = w1 - w2
Weight of water displaced by water = Weight of beaker and water - weight of the beaker
                                                          = w4 - w3
The loss in weight of the stone w1 - w2 = Weight of water displaced by the stone w4 - w3
                                               Up-thrust  = Weight of liquid displaced

Hence, it found that up-thrust is equal to the weight of water displaced by it.

Density: 
Density is defined as the mass per unit volume. Its is scalar quantity. Its SI unit is kg / m3. Mathematically,
                                             Density $D=\frac{M}{V}$
Relative density: 
Relative density is defined as the ratio of density of a substance to the density of water at 4°C.
Mathematically,
                                             Relative density \[\text{R}\text{.D}=\frac{\text{Density of substance}}{\text{Density of water at 4 }\!\!{}^\circ\!\!\text{ C}}\]
Relative density has no unit because it the ratio between two densities.

Meaning of Relative Density:

• If a substance has relative density less then 1, it will float in the liquid taken.
• If a substance has relative density equal to 1, it will float with completely immersed in the liquid. 
• If a substance has relative density greater then 1, it will sink in the liquid.  

Law of flotation: 
When a body is immersed  in a liquid experiences two types of forces. They are:

        i.The force of gravity directed vertically downward.
        ii.The up thrust directed vertically upward.

Due to the action of these two forces, a body moves in the direction of greater force. There will be three possible cases if an object is immersed in liquid:

1. If the weight of an object is greater than up-thrust, the body will sink to the bottom.
2. If the weight of an object is equal to the up-thrust, the body will remain anywhere inside the liquid.
3. If the weight of an object is less than up-thrust, the body will rise to the surface of the liquid and floats. 

Principle of flotation:
Principle of flotation states that a body floats in liquid if it can displace the liquid equal to its won weight i.e
Weight of floating body = Weight of the liquid displaced = Up-thrust.

When a body is immersed in a liquid, it experiences two type of forces:
       a. Up-thrust: Acting in upward direction.
       b. Gravity: Acting in downward direction.
Due to the action to these two forces, a body will move in the direction of greater force. According to the resultant of the forces, there are three cases:
      i. If the weight of an object is less than up-thrust the body will floats on the surface
         of the liquid in which it is immersed.
      ii. If the weight of an object is equal to the up-thrust, the body can be
          in equilibrium condition at any point in liquid.
      iii. If the weight of an object is greater than up-thrust, the body
           sinks to the bottom
Hydrometer: 

Hydrometer is an instrument used to measure the density of various liquid, based on the principle of flotation. There are two types of hydrometers.They are constant immersion hydrometer and constant weight hydrometer. 
a. Constant weight or variable immersion hydrometer: The hydrometer which measures the density by observing the scale of he floating neck is called constant weight hydrometer. It consists of a bulb containing mercury of lead shots to keep it upright while floating. The stem is unevenly calibrated in kg/m3 or g/cm3 units of density. The numbers denoting density in the stem are bigger at the bottom, decreasing upward because a hydrometer sinks less in liquids having more density and sinks more in liquids of less density. 
b. Constant immersion or variable weight hydrometer: The hydrometer which measure the density by adding the weights to immerse to the constant level is called constant immersion hydrometer. It measures the relative density. It is also called the Nicholson hydrometer. It is made to sink to the same level in the water as well as in the liquid by placing weights on its pan at the top so that it displaces the same volume of liquids.
Atmosphereic pressure: 
The pressure exerted by column of air on unit surface area is called atmospheric pressure. It is measured by barometer. Atmospheric pressure can not be changed by us. The atmospheric pressure at sea level  is considered as normal or slandered pressure. Its value at sea level is about 101300 N per meter or 760 mm of Hg.
Air pressure: 
It is the pressure exerted by the air enclosed in a container. It is measured by manometer. Air pressure inside the enclosed container can be changed.
Barometer:
A barometer is an instrument that is used to measure the atmospheric pressure of certain place. There are two types of barometers, a. Mercury barometer (or  Fortin's barometer )  and   b. Aneroid barometer.
A simple barometer consists of a long glass tube filled with mercury and turned upside down in a container of mercury. It works by balancing the mercury level inside the glass tube against the air pressure outside. The level of mercury in the tube gives the measurement of the air pressure.
Syringe: 
A syringe is a medical instrument which is used to draw blood out from a body and to inject medicine through blood. It consists of three parts; piston, barrel and needle. It is made up of glass or plastic. It has a scale on the barrel that indicates the volume of liquid inside it.
When piston is pulled outward keeping needle inside the medicine or liquid, a partial vacuum is created inside the barrel. As a result, there is low pressure inside it so liquid or medicine flows into the the syringe. Likewise, When the piston is pushed inside, there is high pressure in the barrel and pushes the liquid or medicine out of the syringe.
Air Pump: 
Air pump is an instrument used to pump air inside a tube.
Water Pump:
A water pump is an instrument that is used to pull under-ground water. 

Read More